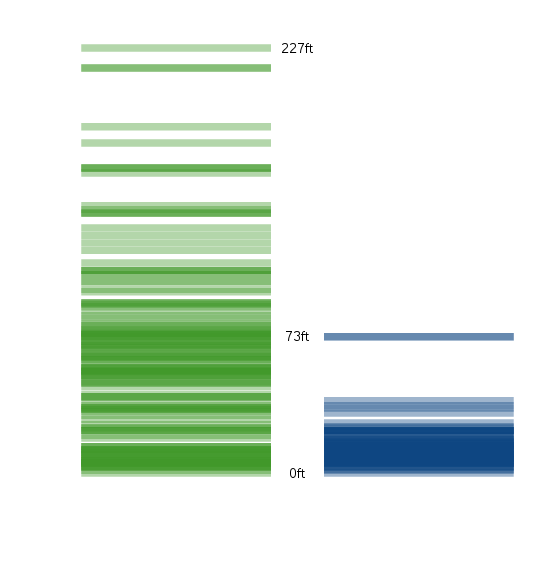决策树入门

一、基本概念

机器学习是指，通过统计学方法，自动找出数据的模式。通俗地说，就是让机器具备分析能力。

为了实现这个目标，需要有两样东西。

• 分析模型
• 已经处理好的数据

通过已经处理好的数据，调试模型的参数，这个过程叫做“模型训练”（Model training）。

等到训练完成，就可以将未处理的数据放入模型，自动运算得到结论。这个过程就是机器学习。

二、分类问题

机器学习要解决的基本问题之一，就是分类（classification），将一堆数据自动分成A类、B类、C类等等。

决策树（decision tree）就是用来解决分类问题的一个模型。它能够通过一系列判断，正确地识别数据类型。

为了做到一点，必须先有一个已经完成分类的数据集，用来训练模型。

三、洛杉矶还是纽约？

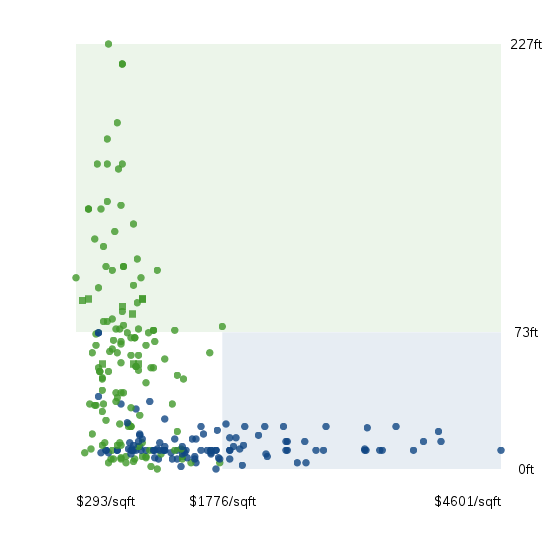
下面是一个房产分类的例子，你有一个房产的基本数据，就是不知道它到底是在洛杉矶，还是在纽约。机器会告诉你答案。

为了做到这一点，必须先训练模型。

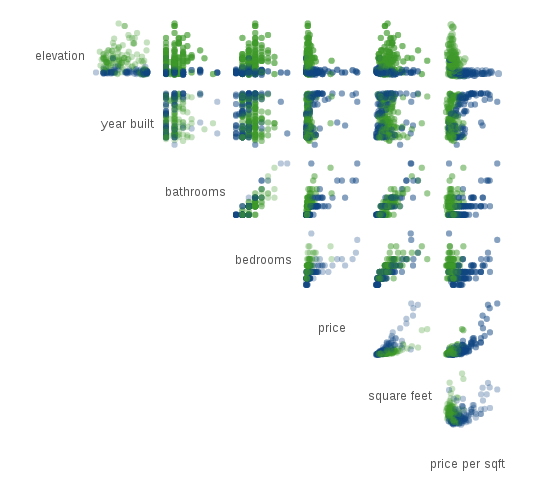
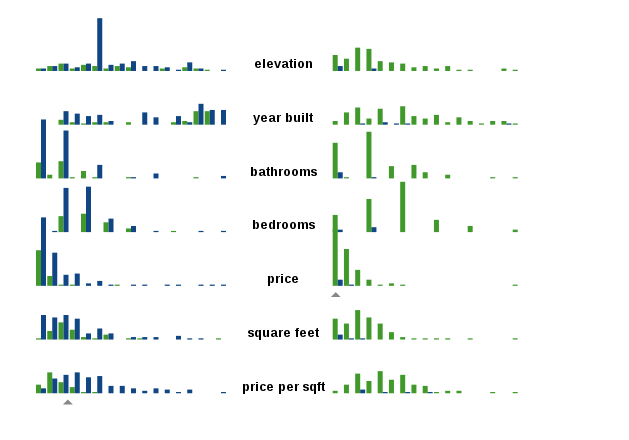
我们的训练数据集，是一批这两个城市房产的统计数据，每个样本有七个指标。

• 海拔高度（elevation）
• 建造年份（year build）
• 卫生间数量（bathrooms）
• 卧室数量（bedrooms）
• 总价（price）
• 面积（square feet）
• 单价（price per sqft）

这七个指标就是一个房产的特征点，又称为维度（dimension）。用统计学语言，就是这个数据集是一个七维数据集。

四、第一轮判断

首先，我们尝试从第一个维度“海拔高度”判断，能不能识别房产所在的城市。

由于洛杉矶多山，房产的海拔较高。因此，只要房产的平均海拔高，就判断这所房子在洛杉矶。

我使用最简单的公式，计算一个门槛值。

分类门槛 = （洛杉矶房产的平均海拔 + 纽约房产的平均海拔 ） / 2

最后得到的门槛值是73英尺（约22米），即如果一个房产的海拔高度超过73英尺，就判断这所房子在洛杉矶，否则就是在纽约。

这样分类并不是完全准确。不难想到，高海拔的纽约房产分到了洛杉矶，低海拔的洛杉矶房产分到了纽约。因此，第一轮判断还不够，单一特征不足以得到正确结果。所以，还要进行第二轮判断。

五、第二轮判断

第一轮判断已经将训练数据集分成了两半（高于73英尺的房产和低于73英尺的房产）。我们依次对这两个子集进行第二轮判断。

这次选择的维度是单价。还是使用前面的公式，统计发现，对于海拔高度低于73英尺的房产，单价的门槛值是每平方英尺1776美元（纽约较贵，洛杉矶较便宜）。

所以，海拔高度低于73英尺的房产，又被分成两类。

• A类：单价小于1776美元的房产
• B类：单价大于1776美元的房产

对于A类来说，由于两个门槛值判断结果一致，因此该房产位于纽约的可能性较高。对于B类来说，由于两个门槛值的判断结果不一致，位于纽约的可能性就低一些。

但是，这两个分类都有可能混入错误的结果，因此还需要更多轮次的判断。

六、后续判断

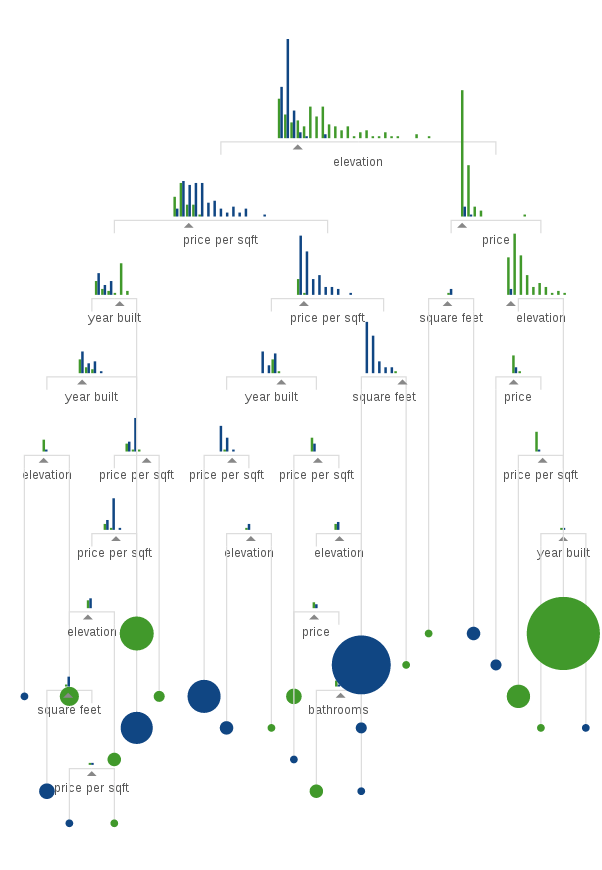
经过前面两次决策，所有数据现在被分成四类。

只要其中有一类还存在错误的分类结果（纽约的被分到洛杉矶，或相反），那么就继续对该分类进行下一轮判断，直到将所有数据正确分类为止，否则该分支就不再往下计算了。

由于还剩下五个维度没有用到，这个决策树最多可以有七层。

经过七层的决策树，依然有可能无法对数据分类。比如，如果某个洛杉矶房产的七个指标，与纽约的房产完全一致，那就会分类失败。

另外，这七个维度的分类能力是不同，有的维度分类效果较好（可能一轮判断就够了），有的维度的分类效果较弱差，甚至具有负效果（即会干扰正确分类）。统计学的一个重要课题，就是找出分类效果最好的那些维度，本文不涉及这方面的内容。

七、完成训练

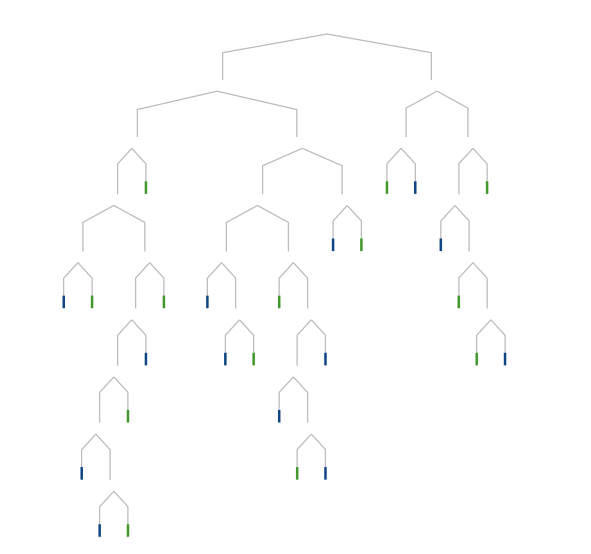
假定经过7轮的训练，所有数据都正确分类了。我们就得到了下面的决策树模型。

整棵数的每个子树节点，都有某个维度的门槛值作为判断标准，决定一个数据到底应该通过左子树，还是右子树。

以后，新的数据进来，只要放到这棵决策树里运行一遍，就能知道它到底在洛杉矶，还是在纽约。